2025年の算数3です。

円柱の水そうに水が入っています。この水そうの底までおもりをしずめます。
水そうの高さは十分にあり、水があふれることはありません。

(1)下のような円柱のおもりを2通りの方法でこの水そうの底までしずめて、横から見たところ、下の[図1][図2]のようになりました。この水そうの底面の半径は何cmですか。

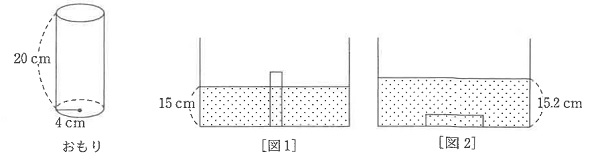
(2)このおもりを[図3]のように、たてに5本しずめると、水面の高さは何cmになりますか。

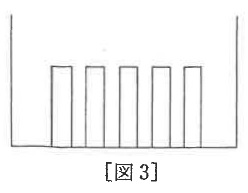
(3)このおもりを(2)と同じように、たてに10本しずめると、水面の高さは何cmになりますか。

【解説と解答】
（１）
図１は水の体積＋円柱の底面積×15cm＝水槽の底面積×15cm
図２は水の体積＋円柱の底面積×20cm＝水槽の底面積×15.2cm
円柱の底面積×５cm＝水槽の底面積×0.2cmなので、
円柱の底面積：水槽の底面積＝1：25
水槽も円柱なので、半径の比は１：５ですから水槽の半径は
４×５＝20cmです。

（答え）20cm
（２）円柱の底面積を【1】、水槽の底面積を【25】とします。
【25】×15.2－【1】×20＝【380】－【20】＝【360】が水の容積。
円柱５本を図３のように入れると、水が入る底面積は
【25】－【1】×５＝【20】ですから、水面の高さは
【360】÷【20】＝18cm
（答え）18cm
（３）10本だと水が入る底面積は【25】－【10】＝【15】になるので、
【360】÷15＝24cmになり、すべて水没します。したがって円柱の体積を水と同じに考えます。
【360】＋【1】×20×10＝【560】
【560】÷【25】＝22.4
（答え）22.4cm