出願に際して、通知表のコピーを添付しますが、ここで問題になっているのか、指示から考えてやはり出席日数でしょう。

続きを読む →

2024年　雙葉学園　算数２番です。

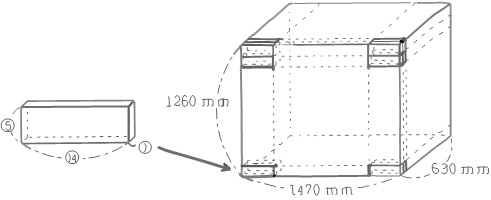
たて630mm、横1470mm、高さ1260 mmの直方体の箱があります。この箱に同じ大きさの直方体のブロックを、図の向きに、箱がいっぱいになるまですき間なく入れていきます。ブロックのたて、横、高さの比は1：14：5です。

箱の中のブロックの数が最も少なくなるときのブロックのたて、横、高さはそれぞれ何mmですか。また、そのときのブロックの数は何個ですか。箱の厚さは考えません。

【解説と解答】
例えば1mm､14mm､5mmとすると、
（630÷１）×（1470÷14）×（1260÷５）＝630×105×252
のブロックが必要になります。
このブロックの数を一番小さくするには、個数の比が
630÷①：1470÷⑭：1260÷⑤＝630：105：252
＝30：５：12ですから、横の数を５個にすればよいことになります。
横を1470÷５＝29４mmにすると、たては21mm、高さは105ｍmになり、これでブロックの数が最小になります。
（630÷21）×（1470÷294）×（1260÷105）
＝30×５×12＝1800個

（答え）たて　21 mm　よこ　294 mm　高さ　105 mm　個数　1800個