ばねに関する問題 | 邦学館　中学受験　理科オンライン塾

2025年　開成中学の問題です。

金属線の太さ(断面の面積)やばねの太さ、巻き数を変えながら図1のようなばねをつくりました｡図2のように、つくったばねの一端を水平な床に固定し、他端におもりをのせてばねの長さの変化を測定しました｡測定の際、ばねは常に床に対して垂直でした｡ばねの重さは無視できるものとして、以下の問いに答えなさい｡

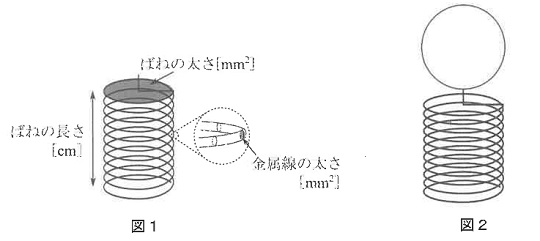
問1 金属線の太さを0.08mm²、ばねの太さを16mm²、巻き数を27回にしてばねをつくり、ばねにのせるおもりの重さを変えてばねの長さを測定しました｡表1はその結果を表しています｡｢ばねの長さを1cm縮めるのに必要なおもりの重さ[g/cm]｣を答えなさい｡答えは四捨五入して整数で求めなさい｡このようにして求めたものを、以下では｢ばね定数｣と呼ぶことにします｡

【解説と解答】
10gで0.25cm、20gで0.5cm縮んでいます。
求める値はばねの長さを1cm縮めるのに必要な重さですから、1cm縮めるには1÷0.25×10＝40gです。
（答え）40

問2 金属線の太さを0.12mm²、ばねの太さを16mm²にしてばねをつくり、ばねの巻き数を変えながらばね定数を測定しました｡表2はその結果を表しています｡ばねの巻き数が80回であるときのばね定数[g/cm]を答えなさい｡答えは四捨五入して整数で求めなさい｡

【解説と解答】
表からばねの巻き数とばね定数は反比例しています。
したがってばねの巻き数が80回のときは $\frac{1}{8}$ になるので、243× $\frac{1}{8}$ =30.375≒30
（答え）30

問3 ばねの太さを9mm2、巻き数を60回にしてばねをつくり、金属線の太さを変えながらばね定数を測定しました。表3はその結果を表しています。ばね定数が121.5 g/cm であるときの金属線の太さ[mm2]を答えなさい。答えは四捨五入して小数第2位まで求めなさい。

【解説と解答】

金属線の太さが3分の4倍になると、ばね定数は9分の16倍、2倍になると4倍になっています。
54：121.5=4：9ですから、金属線の太さは $\frac{3}{2}$ 倍にすればよいので、0.09× $\frac{3}{2}$ ＝0.135≒0.14

（答え）0.14mm²

問4 金属線の太さを0.30mm2、巻き数を50回にしてばねをつくり、ばねの太さを変えながらばね定数を測定しました。表4はその結果を表しています。ばねの太さが81mm2であるときのばね定数[g/cm]を答えなさい。答えは四捨五入して整数で求めなさい。

【解説と解答】

ばねの太さ	9	36	144	255
	3×3	6×6	12×12	15×15
ばね定数の割合	1	$\frac{1}{8}$	$\frac{1}{64}$	$\frac{1}{125}$
ばね定数	720	90	11.25	5.76

となるので、ばねの太さがn×n倍になると、ばね定数の割合は $\frac{1}{n}$ × $\frac{1}{n}$ × $\frac{1}{n}$ になります。

81mm²は9mm²の3×3倍なので、ばね定数は $\frac{1}{27}$ になるから、720÷27＝26.666≒27g/cm
（答え）27g/cm

問5 問2～問4の結果から、金属線の太さを0.16mm2、ばねの太さを36mm2、巻き数を25回にしてばねをつくったときのばね定数[g/cm]を答えなさい。答えは四捨五入して整数で求めなさい。

【解説と解答】
1)　巻き数とばね定数は反比例する。
2)　金属線の太さがn倍になると、ばね定数はn×n倍になる。
3)　ばねの太さがn×n倍になると、ばね定数の割合は $\frac{1}{n}$ × $\frac{1}{n}$ × $\frac{1}{n}$ になる。

問1から金属線の太さが0.08mm²、ばねの太さが16mm²、まき数27回の時ばね定数は40g/cmでした。
まず巻き数を25回にすると、 $\frac{25}{27}$ になるから、反比例なので、40× $\frac{27}{25}$ ＝43.2
金属線の太さが0.16mm²なので、2倍だから、4倍になるので43.2×4＝172.8

ばねの太さが36mm²なので、 $\frac{9}{4}$ 倍になるから $\frac{2}{3}$ × $\frac{2}{3}$ × $\frac{2}{3}$ ＝ $\frac{8}{27}$

172.8× $\frac{8}{27}$ ＝51.2≒51
（答え）51g/cm

問6 輻8.7cmの箱の中に問1で使用したばね3本と幅1.1cmの仕切りを入れたところ、図3のように静止しました。図3は箱を上から見たもので、右側の2本のばねは同じ長さになりました。仕切りの左側のばねの長さ[cm]を答えなさい。答えは四捨五入して小数第1位まで求めなさい。

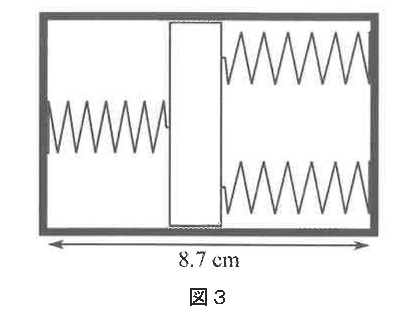
【解説と解答】

問1のばねは、自然長が5cmで10gについて0.25cm伸縮します。
8.7ー1.1＝7.6cmが3つのばねの合計ですが、右側にかかる力を【20】gとするとそれぞれに【10】gかかるから右側のバネの長さは5－【0.25】
左側には【20】がかかるので、5ー【0.25】×2＝4.5－【0.5】　合計10－【0.75】＝7.6
2.4÷0.75＝3.2となるので、5－3.2×0.5＝3.4
（答え）3.4cm

問7 問1で使用したばねをばねaとし、ばねaの巻き数を54回にしたものをばねbとします。厚さと幅が変わらない重さ50gの板の両端A、Bをばねαとばねβで支えました。板の上のCに重さ140 g の球をのせたところ、図4のように板は水平になり、球は板の上で静止しました。「AからCまでの距離」:「CからBまでの距離」を最も簡単な整数比で答えなさい。ただし、おもりをのせないときのばねの長さは、ばねの巻き数に比例するものとします。

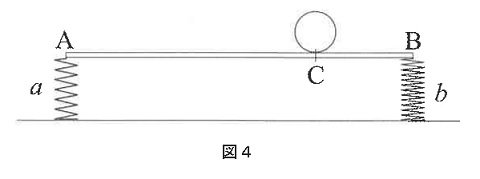
【解説と解答】
問1で使用したばねは、巻き数が27回でしたから、巻き数を54回にすると、ばね定数は半分になるので、ばねbのばね定数は20g/cmです。
最初の長さは巻き数に比例するので、ばねaの自然長が5cmに対してばねbの自然長は10cmです。
したがってばねbを5cmにするために5cm縮めないといけないので、20×5＝100g　さきにBにかけます。
さらにaとbのばね定数の比は2：1になるので、同じ割合で縮めるには2：1の重さが必要になります。
板は50gですから、25gずつAとBにかかります。
Aに【2】、Bには【1】+100ｇですが、板の重さを引くので、
【2】－25+【1】＋75＝【3】＋50＝140から【1】＝30g
したがっておもりはAに30×2－25＝35ｇ　Bには30＋75＝105ｇがかかるのでAC：CB＝105:35＝3：1
（答え）3：1